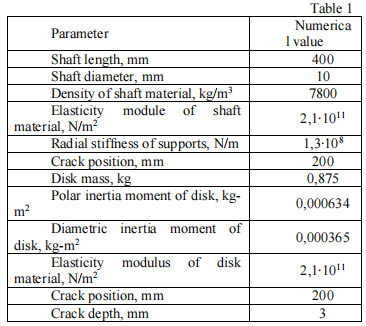
hera 101;&#EYoung Modulus.-Iakselin osan halkaisraalinen inertia-hetki,-m YLImh – hetkellisen jäykkyyden kerroin vastaavassa linkkissä, joka vastaa täysin avointa crackia. Yhtälössä on kaksi summands – joustavuus, joka liittyy halkeamaan ja säteen joustavuuteen ilman crackia.Se
On huomattava, että säteen muodosta, rajaolosuhteista ja murtuman sijainnista riippumatta sen vaikutus yleiseen säteen joustavuuteen riippuu vain kertoimesta m YLIma ,eli ensimmäiset huippukokoukset. Kun säde pyörii, joustavuus crack-osiossa muuttuu, kun se on käynnissä.Me saamme seuraavat:hera 101;
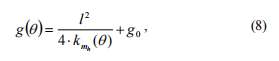
m Lä&#säteen joustavuus ilman halkeamaa, (b) q)=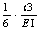 -mmhhetkellisen jäykkyyden nykyinen kerroin annetussa kohdassaqMitä? -Integring kaksi yhtälöt (5) ja (7), saamme:hera101;Kun yhtälö (6) otetaan huomioon, saamme muutoksen lain momenttien jäykkyys riippuen erotuksesta vaiheiden
-mmhhetkellisen jäykkyyden nykyinen kerroin annetussa kohdassaqMitä? -Integring kaksi yhtälöt (5) ja (7), saamme:hera101;Kun yhtälö (6) otetaan huomioon, saamme muutoksen lain momenttien jäykkyys riippuen erotuksesta vaiheiden
a q
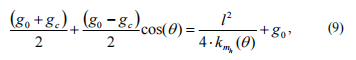
:Vastaavan linkin saatu hetkellinen jäykkyys riippuu ainoastaan akselin halkaisijasta, materiaalista ominaisuuksista ja halkeaman syvyydestä.Vaihto kuilun crack-asennossa, kuilun ominaisuudet, mukaan lukien tukiyksiköt, eivät muuta vastaavan link in (on) hetkellistä jäykkyyttä (on)&#edellyttäen, että osa crack pysyy sama missä tahansa osassa osassa, jossa halkeama, jota varten se olisaatu).Takaisin jäykistys matriisi saatu aikaisemmin, sen jäykkyys kertoimet voidaan kirjoittaa seuraavasti: hera
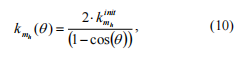
101; m
YLI
ee , m YLI
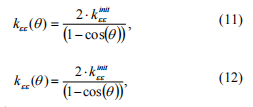
Hh täysin avoimen halkeaman vastaavien akseleiden hetkellisen jäykkyyden alkuperäiset arvot&#Mitä? Euroopan yhteisöjen komissio mYLI ee,mYLI -Hhlaskenta voidaan ratkaista kahdella tavalla.Ensimmäinen on se, että FEM-ohjelmassa lasketaan ajan jäykkyys.Toinen on se, että käytetään teoriaa murtumien mekaniikasta.Se antaa mahdollisuuden laskea avoimen crackin paikallisen joustavuuden kertoimien arvot, jos sen geometria, akselin halkaisija ja materiaalin ominaisuudet ovat tiedossa [7,10].
Algoritmi, jolla simuloidaan roottorijärjestelmää crackin kanssa Seuraavat vaiheet olisi läpäistävä, jotta saadaan kertoimet hetken jäykkyys crack.1. Koko roottorimalli on luotu yhdessä erityisohjelmista, joilla on tarkoitus analysoida roottorin dynamiikkaa (esim.esimerkki, Dynamics R4).2. Murtoa sisältävä roottorin osa on korostettu. 3. Crack jakaa akselin osan kahteen osajärjestelmään.Linkki, jota muuttujan matriisi kuvaajäykkyyden kertoimetAnteeksi.K (q
,
j)
by
Mitta 6x6 asetetaan osajärjestelmien väliin.
4. Hetken jäykkyyden alkukertoimet
m
YLI
ee ,mYLIHhavoimen crackin osalta saadaan annetuilla menetelmilläYlhäällä.Nämä tiedot ovat alustavia laskelmia varten.Stiffness matriisi kertoimet linkki simuloiva crack lasketaan samalla integroidaan liikkeen yhtälöt
Jokaisen roottorin järjestelmän osaltaqMitä?Epälineaarisessa yhtälössä, joka kuvaa epälineaarista dynaamista malliaroottorijärjestelmän on täytettävä seuraavat vaatimukset: hera101;Anteeksi.Lä ]
– inertian kertoimien matriisi;
Anteeksi. C ]
– vaimennus- ja gyroskooppikertoimien matriisi;Anteeksi.K
]
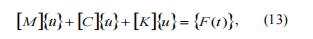
III:n matriisi jäykkyyden kertoimet; QFontDatabase&#mäm,QFontDatabasemäm,QFontDatabasemäm– tärinän kiihtyvyyden, värähtelynopeuksien ja tärinän siirtämisen sarakkeet vastaavasti;QFontDatabase-F(Lä)äm&&mahdollisesti dynaamisen kuormituksen tyypit– sisäiset ja ulkoiset.Saman linkin Stiffness matriisi voidaan jakaa kahteen osaan: vakio ja muuttuja, ja seuraavat ovat totta:Anteeksi.&K C] on sisällytetty yleisen jäykkyyden matriisiin, joka onAnteeksi.K]järjestelmä.Matrix([q j] n,Kon käytetty laskettaessaei-lineaarisen yhteyden reaktiot:-hera101;
m rxLanguage ,
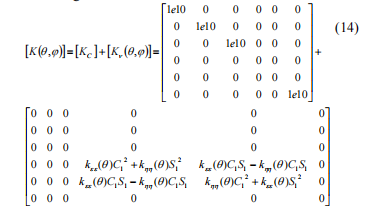
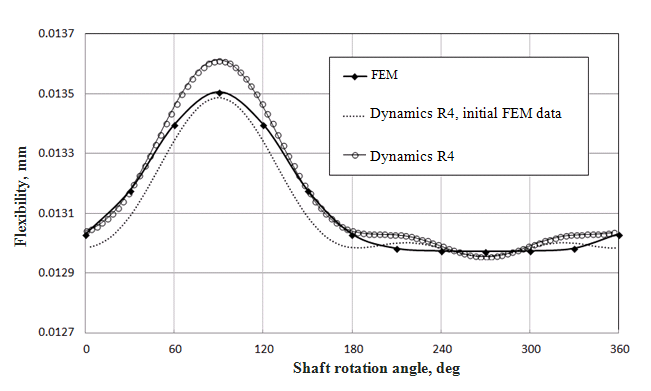
m yy– mukohtien vuorottelut vastaavien akseleiden ympärillä.Lopullinen liikkeen yhtälö järjestelmä on seuraava:Annettu yhtälö voidaan ratkaista numeeristen menetelmien, kuten RungeKutta menetelmä, Newmark menetelmä, jne.Ehdotetun algoritmin asianmukaisuus on tehty vertailemalla näiden kahden algoritmin joustavuuttatukipalkki, jossahalkeama, joka on saatu finiteelementtijärjestelmä ja Dynamics R4:n oletetun algoritmin mukaan.Tehtävänä on laskea sirpaleen taipuminen yksikön voimalla crack-osuuksissa eri vaiheiden osalta crack in ja voiman välillä.Kuva 3 osoittaa ehdotetun algoritmin tarkastuksen tulokset.Vertaillaan kolmea tulosta:joustavuus lasketaan käyttäen finite element menetelmää (FEM).Sädettä, jossa on halkeama, koskevan mallin radikaali joustavuus lasketaan FEM:ssä
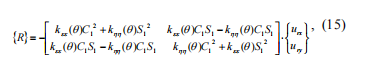
järjestelmä, joka koskee crackin koko kulmasijaintien aluetta;&#joustavuus lasketaan käyttäen Dynamics R4, alkuperäiset tiedot saadaan FEM.Hetken alkuarvotjäykkyys täysin avoimelle crackillem YLIee, mYLI
Hhovat saatu ratkaisuyhtälö (7) varten
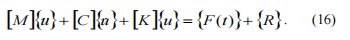
m-YLI
mh-ja säteen joustavuus säteen kanssa crack
gc-vastaava suunta lasketaan käyttäen FEM:ää (FEM).Välittömän kulman crack-position hetkellinen jäykkyys muuttuu minimistä enimmäistasolle (10) lainsäädännön mukaisesti ja
joustavuus lasketaan käyttäen Dynamics R4:ää.Alustavat tiedot hetkellisestä joustavuudesta täysin avoimessa crackissa
-m-ee
YLI , m-Hh
YLIjotka on saatu analyyttisesti käyttäen murtuman mekaanikkojen algoritmeja [7, 10].Hetken joustavuuden arvo, kunKeskimääräisten crack-kulmien positiot muuttuvat minimistä enimmäistasolle lain mukaisesti (10).Kuva 3 Säkkien joustavuuden muutos crack-lohkossa kierrosta kohti FEM:n laskennassa saadut tuloksetDynamics R4:n malli ja mallit ovat lähellä.Analyyttisesti saatujen alkuolosuhteiden perusteella saatujen tulosten laskeminen poikkeaa FEM-tuloksista alle 1%:sta.Samaan aikaan alkuperäinen jäykkyys lasketaan analyyttisesti paljon nopeammin kuin FEM-laskelma, ja se vaatii vähemmän työaikoja ja niin helpompaajaKäyttö. Roturin geometria ja parametrit, joissa on halkeama Murtoa sisältävän roottorin geometria on valittu näyttämään, että algoritmi toimii parhaalla mahdollisella tavalla, taulukko 1.keskuslevyllä varustettu roottori, jonka tukirakenteet on sijoitettu akselin päähän.② ②②②
② ②-②②②②②②②②② ②
②
② ② ②-②-②-②
②
② ② ②