Introduction
- tärkeä suuntaan tärinän diagnostiikassa ilmailun kaasuturbiinimoottorit ja Turbokoneiden on diagnostics mallinnuksen avulla. Mallinnus antaa mahdollisuuden yhdistää läsnänoin erilaisia koneen vikoja merkkejä sen läsnä värähtelysignaalin. Yksi tällaisista virheistä on halkeaman esiintyminen akselit ilmailun moottoreiden ja Turbokoneiden joka on unallowable. Joten tärkein tehtävä diagnostisen järjestelmän on havaita halki ajan ja ennustaa sen etenemisestä.
Appearance halkeaman roottorin johtaa paikallisen jäykkyyden pieneneminen. Arvo jäykkyyden menetys riippuu geometriset ominaisuudet halkeaman. Jos staattinen kuormitus, kuten paino voima, crack avaa ja sulkee, kun roottori pyörii. Tämän seurauksena akselin jäykkyys muuttuu kohti sykli. Halkeama roottorin järjestelmä johtaa following muutoksia värähtelevän signaalin [1]:
·increase amplitudin 1x harmonisen pyörimisnopeuden kasvun takia staattisen taipuma aiheuttaman jäykkyyden väheneminen.
·appearance 2x osan pyörimisnopeuden vuoksi epäsymmetrinen roottorin jäykkyyttä.
·appearance on 3х osan pyörimisnopeuden sillä syklinen avaaminen ja sulkeminen halkeaman.
- päätehtävä matemaattinen malli on kuvaus arvosta ja laki paikallisen muutoksen jäykkyys
- paikka, joe halkeama tapahtuu harkitsevat monia tekijöitä kuin mahdollista.
There useita lähestymistapoja simuloida halki. Yksinkertaisimmassa tapauksissa halkeaman simuloidaan lasku säteen jäykkyys koko akselin [2,3,4]. Muissa tapauksissa varsiosan, Snee crack tapahtuu, on replace, d vastaavalla säteen elementti. Kertoimia jäykkyysmatriisi tällaisen elementin lasketaan ottamalla crack huomioon ja muutos kohti sykli. Työssä [5] laskettaessa jäykkyysmatriisi palkin elementin kanssa halki perustuu käyttöön hitaus hetkiä palkin osa huomioon halki. Työssä [6] jäykkyysmatriisi tällaisen elementin lasketaan yhtälöiden mekaniikka kiinteiden elinten tuhoa. Halkeama voidaan simuloida elastinen yhdistävä linkki leikkaukset akselin sijasta sen sijainti ja antaa crack hetkellä jäykkyys [7,8].
Muuta halkeaman jäykkyys riippuen sen avaamiseksi ja sulkemiseksi, kun roottori pyörii, voidaan kuvata matemaattisesti eri tavoin. Yksinkertaisimmassa tapauksessa voidaan olettaa, että halkeama on vain kaksi asentoa: täysin opened tai täysin suljettu, ja vaihe toiminta voidaan kuvata sen jäykkyys muutos matemaattisesti [4].
toimi [3] kuvaa kaikkein leviämistä malleja jäykkyys muutoksen. Yksiniistä on Gasch yhtälö. Muutos
in jäykkyys tapahtuu riippuen välinen kulma vaiheen staattisen voiman ja halkeaman vaihe ja joita kuvataan 17 harmonisia Fourier-sarjan. Samassa artikkelissa antaa Maes&Davies yhtälö, joe jäykkyys muuttuu riippuen kulmasta mukaan kosini lain. Vuonna Yang mallin jäykkyyden muutokset kosinilla lain aste suhteellisen halkeaman syvyyttä.
Tämä artikkeli kehittyy halkeama mallin pohjalta existed lähestymistapoja ja esitetään myös menetelmät joka antaa mahdollisuuden tuoda esiin merkkejä käytetään havaitsemaan sen edellytys roottorin tarkka.
- algoritmi on sisällytetty Dynamics R4 ohjelma [9], joka edustaa oma
system laskemisesta dynaamista käyttäytymistä monimutkaisten roottorin järjestelmiä.
Crack malli
Within hyväksytyistä simulointi käsitys, halkeama akseli malli on korvattu joustava linkki jakamalla akseli kahteen osaan ja kuvataan jäykkyys matriisi, jossa on vaihtuva kertoimia. Jos ei ole crack, kanta yhteensopivuus kunto osien välillä varsiosien on suoritettu, joten kaikki keskinäinen siirtymät ovat kiellettyjä. Esittelemme pyörivä koordinaatisto ηOε makaa halkeaman alueella Kuva 1. Sen alkuperä yhtenevä alkuperästä kiinteän koordinaatistossa XYZ. Akselin suorittaa kaksi ehdotusta - asianmukainen kierto ja prekessiota ympäri Z-akselin ympäri. Kun kuvataan halkeama ajattelemme vain kierto η ja ε akselit. Siirtymät muihin vapauden astetta laiminlyödään.
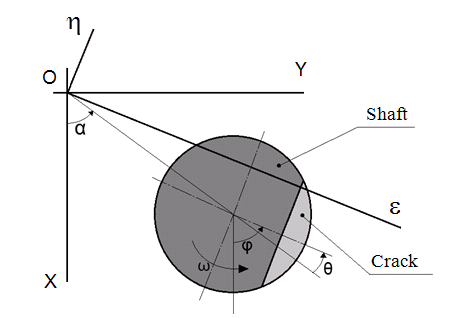
Figure 1. Crack osio
Flexibility matriisi linkin simuloida halkeaman pyörivän koordinaatiston voidaan kirjoittaa following:
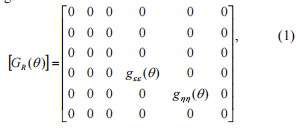
where q =j-a -ero vaiheittain, j -akselin kiertokulma, a -prekessiota kulma; gee (q) ja gHH (Q )-muuttuva coefficients momenttien joustavuuden.
Flexibility riippuu kulmastaqbecause kun akseli pyörii, crack avautuu ja sulkeutuu. Jäykkyysmatriisi saadaan inversion[Ga(q)]matrix, janolla joustavuus kertoimien päälävistäjän johtaa hankkimista jäykkyyskertoimet menee äärettömyyteen. Me raja-arvo tällaisten jäykkyys kertoimien 1е10 N/m; tämä olettamus ei vaikuta merkittävästi tulokseen, eli saadaan
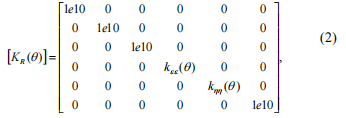
Stiffness matriisi muunnetaan kiinteän koordinaattijärjestelmän seuraavan yhtälön avulla:
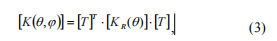
, joe[T]-rotaatiomatriisi (4), SneeC1=\\ aliupseereista (j)S1=sin (j).
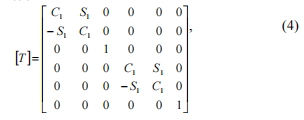
kertominen matriisin vastaavasti yhtälössä (3) saadaan:
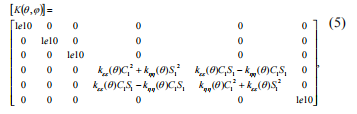
suorittaa joitakin muutoksia, jotka antavat mahdollisuuden siirtää yksinkertaisempaan kuvaus halkeaman stiffness matriisi ja algoritmi sen kertoimien hankkimista. Vastaten Maesin malli, se may voidaan olettaa, että säteittäinen joustavuus pyöreä palkin kanssa halki muuttuu minimistä maksimiin arvon kosinin laki.
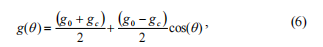
, jo &101;#g0joustavuutta säteen ilman halkeaman (minimiarvo),-gcjoustavuutta säteen avoimen- crack (maksimiarvo).
Yritämme korvata halkeaman, jonka saranan kanssa hetki jäykkyys kinit mH . Palkki reunaehdot olisi tarjota statical definability kuten se on esitetty kuviossa 2.
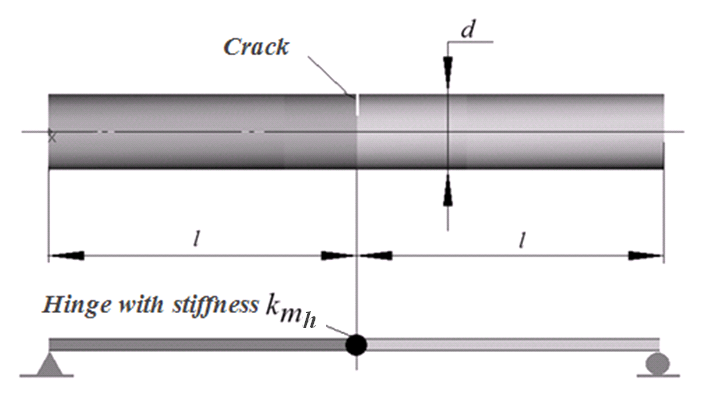
Figure 2 . korvaaminen halkeaman saranan
laitteeseen säteittäinen joustavuus esiin kuilun osassaan avoin särö saadaan:
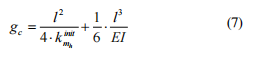
wher &101;#eYoungin moduuli-idiametraaliset hitausmomentti akselin osio,-k init MH - kerroin hetkellä jäykkyys vastaavan linkin, joka vastaa täysin auki halki.

