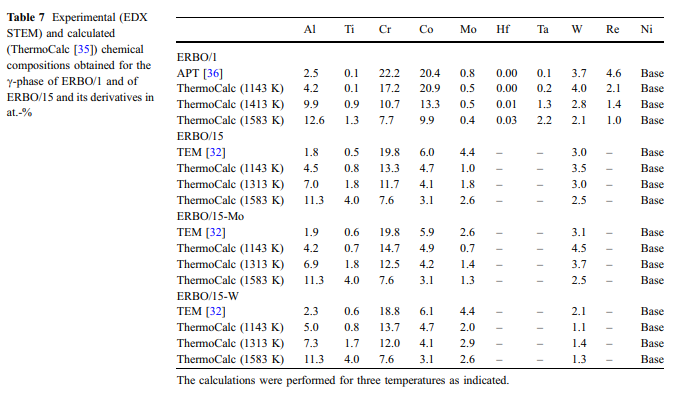
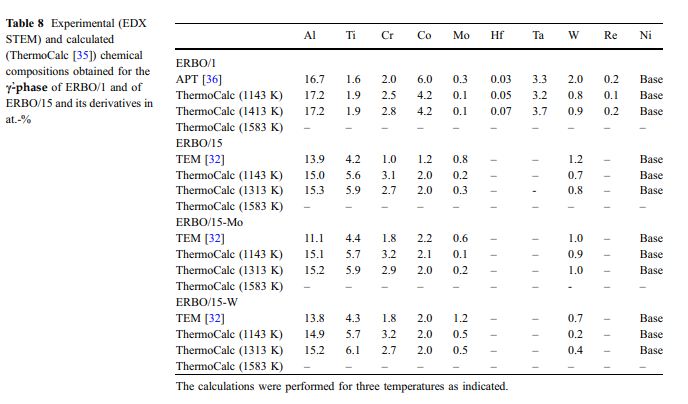
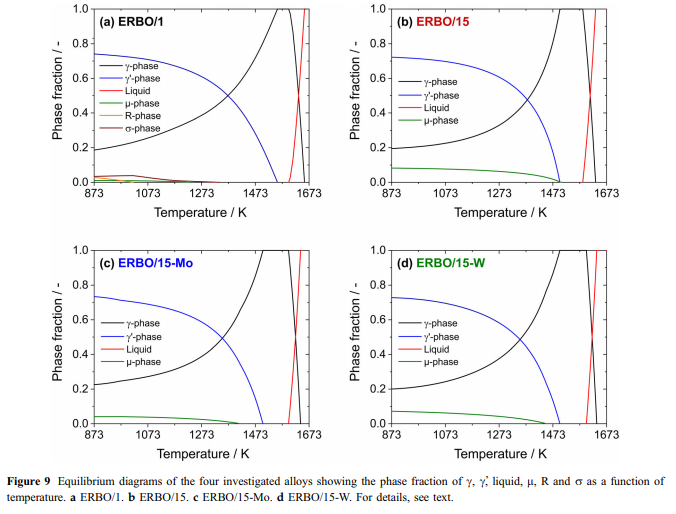
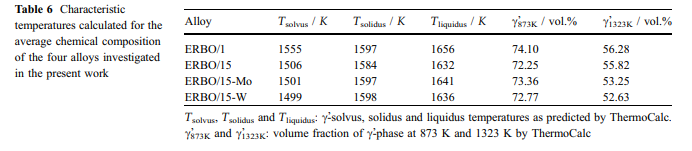
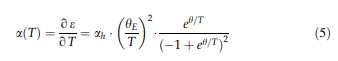Calculated ja mitattu vaihe koostumukset: koostumukset c-ja c-phase (&cc ja cc&)neljä tutkittu seokset mitattiin 3D APT (Erbo 1) [36] ja TEM-EDX (ERBO 15 ja johdannaiset) [32]. Kahden vaiheen kokeelliset tulokset esitetään taulukoissa 7 (C-Phasi) ja 8 (C-&faasi). Taulukot 7 ja 8 sisältävät myös lämpötilat 1143 K (toisen saostuksen käsittelyvaiheen lämpötila kaikille seoksille), 1413 K ja 1583 K (ERBO/1; ensimmäisen saostuksen käsittelyvaiheen ja homogenoinnin lämpötila vastaavasti) ja 1313 K ja 1583 K (Erbo/15 variantteja, lämpötila ensimmäinen saostuskäsittely vaiheessa ja homogenisointi, vastaavasti). Koska C-faasi on pienempi tilavuusfraktio kuin C-Phase, muutokset sen kemiallisessa koostumuksessa&ovat voimakkaampia. Kuvioissa 1 - 10 ja 11, esittelemme C-Phase -koostumuksia taulukosta 7 piirakka-kaavioiksi. Kuvio 10 esittää kokeellisia tietoja, jotka mitattiin kaikillaneljässä lämpöä-trated-seoksissa ennen hiipiä. ERBO-1 (1143, 1413 ja 1583 K) ja ERBO/15 (1143, 1313 ja 1583 K) saadut termocalc-ennusteet on esitetty kuviossa 11. 11./
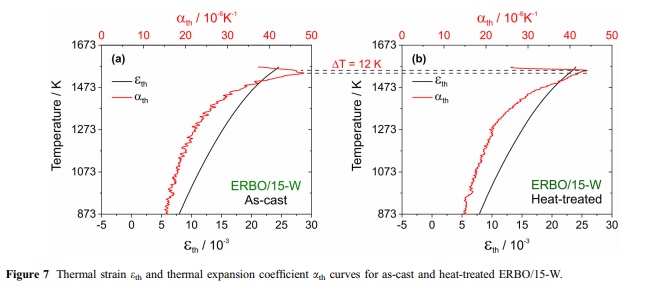
- tiedot esitetään taulukossa 7 ja kuvioissa. 10 ja 11 (c phase) ja taulukossa 8 (c-phase, tiedot esitetään-ilman kuvia) osoittavat, että lisäämällä lämpötilat johtavat kasvavia määriä Ti, AI ja Ta ja samanaikaisesti väheneviä määriä Cr, Co, W ja Re sillä Erbo&1 C/phase. Kuten kuviossa 2 esitetyssä termocalc-tuloksissa voidaannähdä, emäselementin NI määrä kasvaa lisäämällä lämpötila ERBO-1. Sen sijaan, se laskee lämpötilannoustessa sisään Erbo/15.The/ thermodynamic tiedot cja c-phases-taulukossa 7 (ja kuviot. 10 ja 11) ja taulukossa 8, vastaavasti, lisäksi osoittavat, että ThermoCalc tiedot 1143 K (lämpötila viimeksi saostuskäsittely kokeellisten seosten) ja kokeellisesti määritetyt tulokset eivät ole täysin samaa, mutta kohtuullisen lähellä toisiaan sekä metalliseos järjestelmissä. Vain tapauksessa Erbo&15, elementti Mo osoittaa merkittävästi pienemmän arvon laskennassa on 1143 K (1,0 at.%) Kuin kokeessa (4.4at.%)./
discussion elastiset jäykkyydet: Kuten kuviossa 6a-C voidaannähdä, kaikki elastiset jäykkyydet vähenevät lisäämällä lämpötilaa. Tämä johtuu pääasiassa seurauksena ristikkopotentiaalin anharmonisuudesta. Lisääntyvä lämpötila kasvavat lämpörähdistykset johtavat suurempiin sidosetäisyyksiin, mikä johtaa liimauksen vuorovaikutuksen vähenemiseen ja siten elastisten jäykkyyksien vähenemiseen. Elastinen käyttäytyminen Erbo1 ja Erbo/15 on lähes identtinen, Sne/&101, koska tulokset kevyempi Erbo#15 varianteista c11 ja c12 jäävän hieman. Tämä ei vaikuta merkittävästi elastiseen modutiin E \\ 100 [, joka kaikki ovat hyvin lähellä (kuvio 6d). Kuten taulukossa 9 onnähtävissä, SX:n yksittäiset seoselementit eroavat kooltaan, kristallirakenne,nuori moduuli, elektroniikka ja sulamispiste [48-51]. Kuvio 6d osoittaa, ettänykyisessä työssä käsiteltyjen seoskemian muutokset eivät vaikuta voimakkaasti elastisiin ominaisuuksiin. Tämä on sopusoinnussa Demtro'der et ai. [41], joka osoitti, ettänykyisessä työssä harkittujen metallisikoostumusten suuremmat vaihtelut eivät vaikuta voimakkaasti SX:n elastisiin ominaisuuksiin. Yhden kidelin joustava käyttäytyminen heijastaa suoraan sen liimausjärjestelmän anisotropiaa. Jälkimmäistä ohjataan pääasiassa lähimpään/neighbor -yhteyksien tyypin,numeron ja paikkatietojärjestelyn mukaan kristallirakenteeseen. Koska rakenteiden Ni-base SX (mukaan lukien c-c '/mikrorakenteet) sekäniiden tärkeimpien kemialliset koostumukset ([62.-% Ni, [11.-% AI) eroavat vain vähän, vuorovaikutusta hallitsevat Ni-Ni ja Ni-AI-yhteydet, jotka johtavat vain pienet vaihtelut makroskooppisten elastisen jäykkyyksiä [42].-
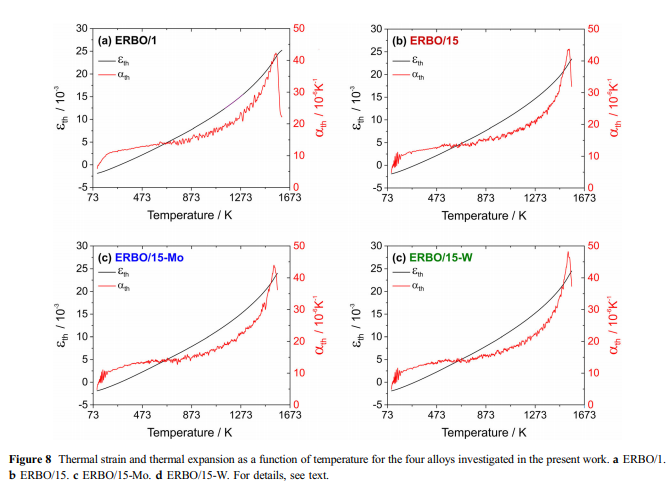
Thermal laajeneminen ja csolvus lämpötiloissa-: lämpölaajeneminen on liitetty materiaalin taipumus muuttaa äänenvoimakkuutta lämpötilannoustessa. Kiteessä tämä liittyy atomien lisääntyvään värähtelevän energian ja ristikkopotentiaalin ei-non&ormonisen muodon. Gru¨-Neisi -suhteen mukaan Aðtþ on verrannollinen lämpökapasiteettiin; siten, terminen kanta eðTÞ voi olla- described integroidusta muoto Einstein malli [52, 53]:
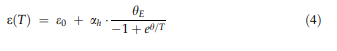
e0 edustaa lähtökanta 0 K, ah tarkoittaa korkeantemperature raja lämpölaajenemiskerroin, ja hän on ekvivalentti Einstein lämpötila. Ensimmäinen derivaatta lämpötilan suhteen tuottaa lämpölaajenemiskerroin:-