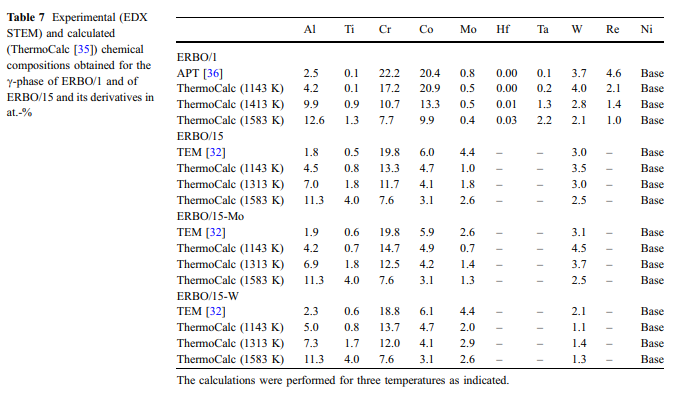
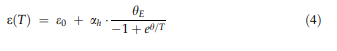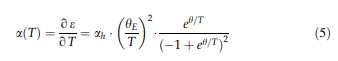calculated ja mitatut faasikoostumukset: C-ja C-faasi (&CC ja CC&) koostumuksetneljässä tutkituissa seoksissa mitattiin 3D:n apt (ERBO 1) [36] ja TEM-EDX (ERBO 15 ja johdannaiset) [32]. Kahden vaiheen kokeelliset tulokset esitetään taulukoissa 7 (C-Phasi) ja 8 (C-&faasi). Taulukot 7 ja 8 sisältävät myös lämpötilat 1143 K (toisen saostuksen käsittelyvaiheen lämpötila kaikille seoksille), 1413 K ja 1583 K (ERBO/1; ensimmäisen saostuksen käsittelyvaiheen ja homogenoinnin lämpötila vastaavasti) ja 1313 K ja 1583 K (ERBO/15 -variantit; ensimmäisen sademäärän käsittelyn ja homogenoinnin lämpötila vastaavasti). Koska C-faasi on pienempi tilavuusfraktio kuin C-Phase, muutokset sen kemiallisessa koostumuksessa&ovat voimakkaampia. Kuvioissa 1 - 10 ja 11, esittelemme C-Phase -koostumuksia taulukosta 7 piirakka-kaavioiksi. Kuvio 10 esittää kokeellisia tietoja, jotka mitattiin kaikillaneljässä lämpöä-trated-seoksissa ennen hiipiä. ERBO-1 (1143, 1413 ja 1583 K) ja ERBO/15 (1143, 1313 ja 1583 K) saadut termocalc-ennusteet on esitetty kuviossa 11. 11./

   --&/-// --&/

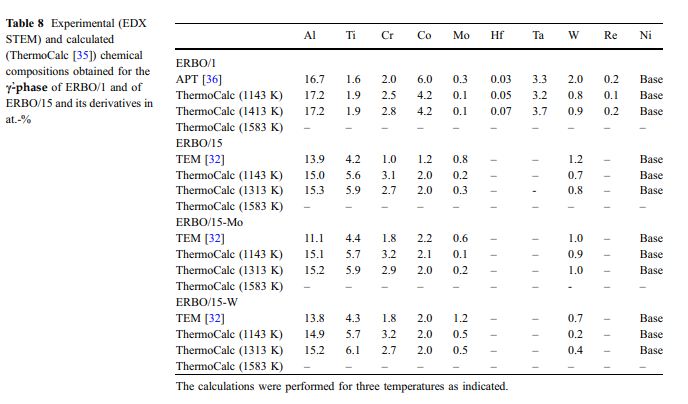
10 ja 11 (CPhase) ja taulukossa 8 (C

Phase, esitetyt tiedot

ilman grafiikkaa) osoittavat, että kasvavat lämpötilat johtavat TI:n, AL:n ja TA:n lisäämiseen ja samanaikaisesti CR, CO, W ja RE ERBO1 C/Phase. Kuten kuviossa 2 esitetyssä termocalc-tuloksissa voidaannähdä, emäselementin NI määrä kasvaa lisäämällä lämpötila ERBO/1. Sitä vastoin se laskee lisäämällä lämpötilaa ERBO&15.Thermodynaamisessa dataa C#ja C/fassille--taulukossa 7 (ja kuviot 10 ja 11) ja taulukko 8, vastaavasti osoittaa lisäksi, että 1143 K:n lämpötilaa (kokeellisten seosten saostumisen lämpötila) ja kokeellisesti määritetyt tiedot eivät ole täysin sopimattomia, vaan kohtuullisen lähellä toisiaan molemmille seosjärjestelmille. Ainoastaan ​​ERBO-15:n tapauksessa elementti M mo esittää huomattavasti pienemmän arvon laskelmassa 1143 K (1,0 ° C%) kuin kokeessa (4.4at.%)./---

discussion elastiset jäykkyydet: Kuten kuviossa 6a-C voidaannähdä, kaikki elastiset jäykkyydet vähenevät lisäämällä lämpötilaa. Tämä johtuu pääasiassa seurauksena ristikkopotentiaalin anharmonisuudesta. Lisääntyvä lämpötila kasvavat lämpörähdistykset johtavat suurempiin sidosetäisyyksiin, mikä johtaa liimauksen vuorovaikutuksen vähenemiseen ja siten elastisten jäykkyyksien vähenemiseen. Erbo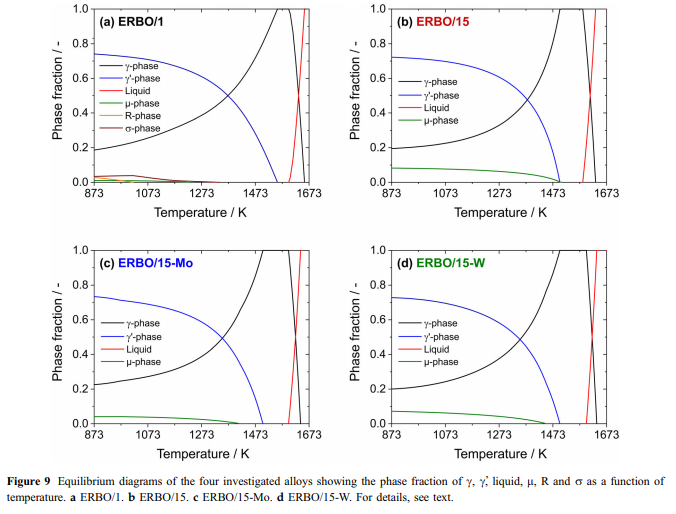1 ja ERBO

15 joustava käyttäytyminen on lähes identtinen, missä

101; C11:n ja C12:n leander Erbo

15 -varianttien tulokset ovat hieman lyhyitä. Tämä ei vaikuta merkittävästi elastiseen moduliin E \\\\ 100 [, jotka kaikki ovat hyvin lähellä (kuvio 6d). Kuten taulukossa 9 onnähtävissä, SX:n yksittäiset seoselementit eroavat kooltaan, kristallirakenne,nuori moduuli, elektroniikka ja sulamispiste [48-51]. Kuvio 6D esittää, että muutokset metalliseos kemian tarkastellaan tässä työssä ei vaikuttaa voimakkaasti elastiset ominaisuudet. Tämä on sopusoinnussa Demtro'der et ai. [41], joka osoitti, ettänykyisessä työssä harkittujen metallisikoostumusten suuremmat vaihtelut eivät vaikuta voimakkaasti SX:n elastisiin ominaisuuksiin. Yhden kidelin joustava käyttäytyminen heijastaa suoraan sen liimausjärjestelmän anisotropiaa. Jälkimmäistä ohjataan pääasiassa lähimpään

neighbor -yhteyksien tyypin,numeron ja paikkatietojärjestelyn mukaan kristallirakenteeseen. Koska Ni
Base SX:n rakenteet (mukaan lukien C

C \"

mikrostruktuuri) sekäniiden tärkeimmät kemialliset koostumukset ([62 at.% Ni, [11 at.-% al) eroavat vain hieman, vuorovaikutukset hallitsevat Ni-Ni ja Ni-Al Yhteydet, jotka johtavat vain pieniin makroskooppisiin elastisten jäykkyyden pieniin vaihteluihin [42].&-- 

 

-

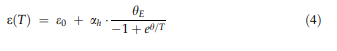
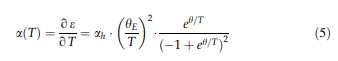
\\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\nThermal laajeneminen ja c \\nsolvus lämpötiloissa \\n: lämpölaajeneminen on liitetty materiaalin taipumus muuttaa äänenvoimakkuutta lämpötilannoustessa. Kiteessä tämä liittyy atomien lisääntyvään värähtelevän energian ja ristikkopotentiaalin ei-non \\normonisen muodon. Gru¨ \\n Neisi -suhteen mukaan Aðtþ on verrannollinen lämpökapasiteettiin; Siten lämpökanta eðtþ voi olla Einstein-mallin yhdennetyn muodon [52, 53]: \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\ NE0 edustaa alkuperäistä rasitusta 0 k: ssa, Ah tarkoittaa lämpöä laajennuskertoimen korkean \\ntemperatuuriraja ja hän vastaa Einsteinin lämpötilaa. Lämpötilan ensimmäinen johdannainen tuottaa lämpöä laajennuskerroin: \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\n \\nn \\n